在TiKV 的多副本机制一文中,我们讨论了 TiKV 集群可以容忍单节点故障,但是如果发生了多个节点同时故障,就可能导致不可用乃至于丢数据了,这个其实也适用于大多数依赖于多副本冗余数据的系统。因此,估算集群中多个服务器同时故障的概率是很有现实意义的,这个问题最简化的形式就是两台服务器同时故障,本文准备做这种情况的概率估算,然后用随机实验的方式加以验证。
概率模型估算
回忆当年《概率与统计》课程,依稀记得说电灯泡的损坏是服从于指数分布的,其分布函数是这样:
$$ P(t) = 1 - e^{-\lambda t} $$
这个公式可以用来计算灯泡寿命小于 t 的概率,其中$\lambda$代表损坏事件发生的频率,即单位时间损坏事件发生的次数。由于指数分布的“无记忆性”,也就是说假设每时每刻发生故障的概率是一样的,这个公式同样也可以用来计算两次故障的间隔。
说点题外小知识点,现实中产品(特别是电子产品)往往是有记忆性的,生命周期的不同阶段发生故障的概率并不完全相同,其规律表现为一条两侧陡峭,中间平坦的曲线,也被称为浴缸曲线。这也符合我们日常生活中的体验,新设备到手有一段“磨合期”,用时间长了有一段“老化期”,而这二者中间是相对稳定的。当然了本文不会考虑这么细,还是用简化模型来进行分析。
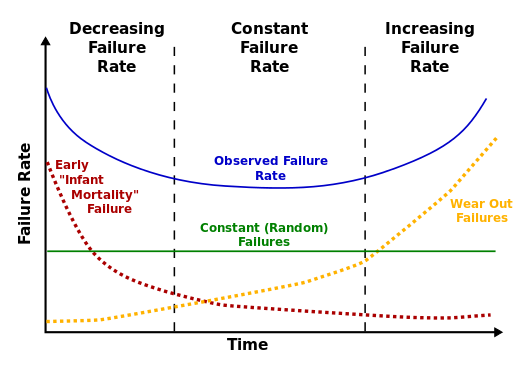
浴缸曲线示意图
为了套用指数分布的公式,我们需要知道服务器的年故障率$\lambda$,这个可以在已有集群上统计出来,也可用参考 Google,微软等云服务厂商给出的相关报告,还可以通过硬件厂商给的 MTBF(平均故障间隔)来进行推算(把时间单位换算成年再求倒数)。
我们假设集群有固定的$N$台服务器,且每台服务器的年故障率都是$\lambda$,如果把集群当作一个整体,其故障的频率就是$N\lambda$,套用指数分布公式,这个集群在时间 t 内发生故障的概率是:
$$ P(Failure(t)>0)=1-e^{-N\lambda t} \tag{1} $$
接下来我们来计算两节点同时故障的概率。要注意此概率与“集群发生两次故障”的概率是不一样的,多了一个“同时”的约束。要知道故障都是一瞬间发生的,那是不是意味着两节点同时故障的概率就是 0 呢?其实也不是。在多副本冗余的场景下,一个节点故障以后,集群需要一个过程来消除这次故障所带来的影响(比如另找服务器补副本),如果下一次故障时影响已经完全消除了,那么数据安全是不受影响的,可以认为是“依次故障”,反之如果影响消除之前发生下一次故障,那么就可能丢数据,我们应该认为这种情况属于“同时故障”。
搞明白这点后,我们可以引入一个新的变量$T_r$表示恢复故障所需要的时间。当一次故障发生之后,$T_r$时间内不发生下一次故障的概率是:
$$ P(Failure(T_r)=0)=e^{-N\lambda T_r} $$
显然,出现两节点同时故障的概率 = 1 - 每次故障后的Tr时间内都不发生下一次故障的概率,而时间 t 内发生故障次数的期望是 $N\lambda t$,因此,时间 t 内出现“两节点同时故障”的概率是:
$$ P(Failure2(t)>0)=1-(e^{-N\lambda T_r})^{N\lambda t} = 1-e^{-N^2\lambda ^2 T_r t} \tag{2} $$
蒙特卡罗方法实验
所谓蒙特卡罗方法,其实就是统计模拟的方法,通过生成随机数进行大量的重复模拟实验,最后在大数定律的作用下,实验结果均值会逼近于期望值。这个方法对程序员来说是特别友好的,接下来我们就尝试用这个方法验证一下上文的概率推导。
为了先大概看一下蒙特卡罗方法是如何工作的,我先写了个简单的框架并验证了几何分布的期望值。代码很简单,模拟逻辑部分包含一个 estimated 表示预估值以及sim()函数运行一次模拟并返回实验结果,main函数就是不断地运行sim()并比较模拟平均值和预估值的差距。下面是一个简单的验证几何分布的例子:
运行结果精简之后如下,能观察到均值很快收敛在 0.5 附近,误差不超过 0.1%。
接下来我们考虑如何用蒙特卡罗方法来模拟服务器故障,思路也比较简单,就是把较长的时间分割成很多段较小的时间$\Delta t$,根据公式(1)可以算出$\Delta t$内每台服务器出现故障的概率,然后就用 for 循环 tick,不断判断每台服务器每段$\Delta t$是否故障。
我先设计了个实验来检查累计的方式模拟结果是不是奏效。设定集群规模$N=20$,故障率$\lambda=0.05$,模拟总 tick 数$totalTick=365\times 24\times 60$,也就是把一年时间分成这么多份,每份是1分钟,然后每次模拟一年的时间并计算故障率,最后与预设的故障率$\lambda$进行对比。
运行结果也是符合预期地收敛到了 0.05 附近,5000 次循环之后误差降到了 1% 以内。
第二次实验模拟了一年时间发生至少一次故障的概率,参数同实验一:
结果显示在此配置下一年内发生故障的概率约为 63.2%,随机模拟也匹配得很好,700 次循环后误差降到了 1% 以内。
最后第三次实验模拟的就是两节点同时故障的概率了,恢复时间 Tr 设置成 24 小时。estimated 根据公式(2)计算。
结果显示发生两节点同时故障的概率约为 0.27%,远小于单节点故障的概率。这次误差收敛得很慢,大约70000次循环之后似乎降到了 1% 以内,主要应该由于概率太小了,大体上误差收敛的趋势还是比较明显的,我就没有继续跑了。
我写文章的时候细想了下,发现实验三的模拟值跟估算值最终应该是会有些误差的。如果在一年的最后一天发生故障,紧接着的下一次故障在 24 小时内,但是是在下一年。这种情况下,估算的时候会算做发生同时故障,但是模拟的时候会忽略掉。不过这种特殊情况对整体的概率影响应该非常有限,我就懒得再重新折腾了。